Pocket strategies: Purposeful Incredulity

Think back to your school years. Think of that one teacher who managed to make every lesson fun and engaging, the one who had a canny way of making even the driest of topics seem worthwhile and interesting. 

How did they do it? 

Personality? Sure, probably. But I think this short post from Dan Meyer may have something to do with it, too. They made the content interesting, somehow. And it wasn't usually by embedding it into a game or puzzle or activity -- it was because they tapped into something genuine. They didn't just pose questions and show us how to find the answers, they made the questions seem worth investigating.

Dan's post calls it "developing the question."

http://blog.mrmeyer.com/2014/developing-the-question-why-students-dont-like-math/

A lesson I observed recently involved the theorem that "the sum of the vertex angles in any triangle is 180 degrees." The lesson involved an informal proof--an activity, wherein students created a triangle of arbitrary size and shape, cut it out, tore off the corners, and rearrange them to form...  a...

"What are we supposed to do with the pieces?" A student asked, mid-lesson. 

Just see what you can notice.

Eventually a few kids got the corners to form a straight angle. Word spread quickly, and before long everyone found they could do it. It's a nifty trick if you haven't see it:

Source: cutoutfoldup.com

But... now what? Because the question was never really developed, there wasn't much of a climax to build to, nor was there much relief when kids had figured out what to do.

But Dan's post got me thinking about that lesson again. How could we develop the question? One way I like to do it is by using what we might call 'purposeful incredulity'. I include it on my list recyclable "pocket strategies" for enriching, extending, or enhancing a traditional lesson.

Here's what purposeful incredulity might look with this interior angle sum lesson:

Teacher: You all know that the sum of the angles in a triangle is... [wait for it...]

Students: "180 degrees."

Teacher: Right. And there's even a cool way to prove it by cutting out a triangle, tearing the corners off, and lining them up to form a straight angle. Check it out...

    (Wait for the "Ooooh...")

Teacher: I know: pretty cool, right?

Teacher: But don't you think that's weird? Isn't it curious that the angles in any triangle have to sum 180 degrees? Any triangle? No matter what size it is? No matter what shape? I never could quite buy it. I mean, if you scale up the sides, you get a bigger triangle right? It's bigger, meaning the area is greater, the perimeter is greater, ... aren't the angles bigger too? (Careful: There's a common misconception about angles that might be worth probing at this point.)

Teacher: If you grab hold of one vertex and slide it around, you start changing the shape. Won't that change the angles? Sure it will. And yet here they are, telling me that the angles will sum to 180?? Why should that be?

Teacher: I think we should try to disprove this... everyone, let's try to make a triangle where the angle sum is not 180 degrees. Here is some paper, scissors, rulers, protractors... let's figure this out!

After some triangle trials and tribulations, some may claim to have a triangle that "breaks" the theorem.

I would anticipate some creative solutions, like B and D, below...

I would expect some flawed counter-examples resulting from imprecise measurements or drawings, based on issues like the ones I wrote about in a related post.

With any luck, someone will start thinking outside the box and come up with a solution like this:

Are those a bunch of 90-90-n triangles? What's the angle sum there?

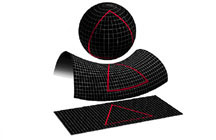
And some might stumble upon a classic result from spherical geometry, such as this triangle with an angle sum of 270 degrees: 

A triangle with 3 right angles!

Aside: On a unit sphere, the area of a spherical triangle may be computed directly from the angle sum. So much for "Area = 1/2 base x height..."

For spherical triangles: Area = AngleSum - π

Think about that for a second. To calculate the area, you measure the angles. Teeny tiny triangles with almost no area have angle sums just slightly greater than 180 degrees. As the triangle grows, so does the angle sum. Hmm.

Others might do some research on their mobile device and come across this...

http://imagine.gsfc.nasa.gov/docs/features/exhibit/map_shape.html

That last one is my favorite. Scientists are actually trying to measure the angles of a really big triangle to determine the physical shape if our universe: spherical, hyperbolic, or flat. 

In fact, it was purposeful incredulity that led to the discovery of non-Euclidean geometries in the first place.

"These discoveries could never have been made without...progressive thinkers who were able to suspend their preconceived notions and think outside of what they have been taught..."

If you try a version of this lesson with your students, or experiment with purposeful incredulity in your teaching, please let me know how it goes!

I'll do the same...