PSTs: "What I will do to make sure my elem students have a good math experience?"

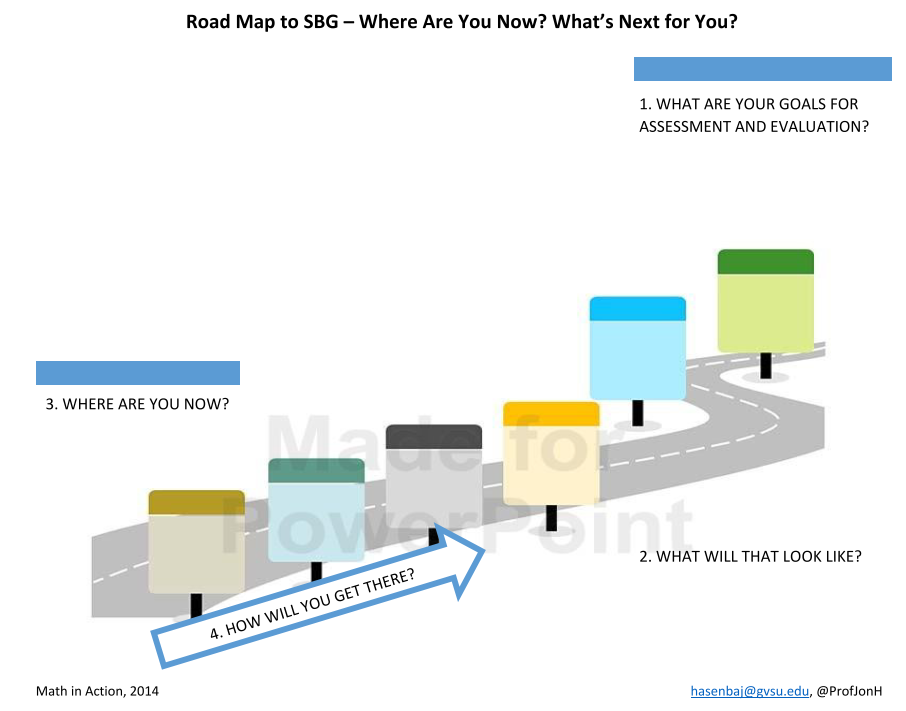
I try to give my students plenty of opportunity to reflect on their growth as we approach the end of the semester. With that goal in mind, I had my students tell me what they remembered about their experiences with mathematics while they were in elementary school. You can read their responses by clicking the image.

Fast forward to the end of the semester. In our last week, I printed out those responses, cut them into slips of paper, and gave one slip to each student at random. They read their quote and talked about it at their table. Then they got up and found a partner ("find someone who has similar shoes") and read each other their quotes while discussing how they wanted their future students to say about their elementary math experiences.

Spurious correlations, three ways

I stumbled across a collection of spurious correlations a while back.

Here is one of them that struck me, in part because the data set links sour cream consumption per capita and motorcycle riders killed in non-collision transport accidents, but also because it is presented in odd sort of way.

Headline: Sour cream consumption linked to greater risk of non-collision transport death by motorcycle.

TT-TNG (F14 edition)

Teaching Tips (from) The Next Generation

Presenting the inaugural edition of... Teaching Tips (from) the Next Generation: a summary of semester-end blog posts written by graduating secondary math teachers at Grand Valley State University.

They share their greatest areas of personal growth and their most powerful teaching strategies from their recently completed student teaching experiences.

• Mr. Snyder: http://snydermathgv.wordpress.com
• Mr. Burdick: http://mitchellburdick.blogspot.com 
• Ms. Jamison: http://learningtoteachorteachingtolearn.blogspot.com
• Ms. Rickard: http://lovetoteachgv.wordpress.com
• Mr. Taylor: http://dataylor92.wordpress.com 

(I will continue to add more as they come in. Last update: 12/1/14 at 12:55pm)

The Equity Principle

Here's a clip from NCTM's webpage on the Equity Principle:

So Equity does NOT mean that every student is treated the same.

That can be tough for new educators, especially here in America where all men are created equal is taken as a "self-evident" fact in our founding documents. (Except...)

Pocket strategies: Purposeful Incredulity

Think back to your school years. Think of that one teacher who managed to make every lesson fun and engaging, the one who had a canny way of making even the driest of topics seem worthwhile and interesting. 

How did they do it? 

Personality? Sure, probably. But I think this short post from Dan Meyer may have something to do with it, too. They made the content interesting, somehow. And it wasn't usually by embedding it into a game or puzzle or activity -- it was because they tapped into something genuine. They didn't just pose questions and show us how to find the answers, they made the questions seem worth investigating.

Dan's post calls it "developing the question."

http://blog.mrmeyer.com/2014/developing-the-question-why-students-dont-like-math/

A lesson I observed recently involved the theorem that "the sum of the vertex angles in any triangle is 180 degrees." The lesson involved an informal proof--an activity, wherein students created a triangle of arbitrary size and shape, cut it out, tore off the corners, and rearrange them to form...  a...

"What are we supposed to do with the pieces?" A student asked, mid-lesson. 

Just see what you can notice.

Eventually a few kids got the corners to form a straight angle. Word spread quickly, and before long everyone found they could do it. It's a nifty trick if you haven't see it:

Source: cutoutfoldup.com

But... now what? Because the question was never really developed, there wasn't much of a climax to build to, nor was there much relief when kids had figured out what to do.

But Dan's post got me thinking about that lesson again. How could we develop the question? One way I like to do it is by using what we might call 'purposeful incredulity'. I include it on my list recyclable "pocket strategies" for enriching, extending, or enhancing a traditional lesson.

Quadrilateral Hierarchies - Productive Struggle

An overarching goal for the semester is to help my pre-service teachers grow more comfortable with "productive struggle" and with persevering on challenging tasks. We worked at it for a long time earlier this semester on problems like the Chessboard Problem, the Cheesecake Task, and many others.

Last week, we moved into Geometry. After spending some time exploring the Van Hiele levels of geometric thought and the kinds of activities that help children progress to higher levels, it was time to put their own geometry knowledge to the test.

In this two-stage lesson, I first divided the class into five teams (of four) and assigned each team a shape class: rectangles, kites, rhombuses, parallelograms, trapezoids (inclusive definition). They were directed to produce a poster with a 2x2 grid with space for examples and properties of general and special members of their shape class.

Here's an example:

Geogebra Tube Links for Mth221

Which quadrilateral am I? (Paul Yu)

https://www.geogebratube.org/student/m51987

Measured kitemaker (Paul Yu)

https://www.geogebratube.org/student/m19458

Triangle Inequality (Todd Smith)

https://www.geogebratube.org/material/show/id/78938

Interesting: Which of the three congruent triangles shown appears to have the most area? The most perimeter?

https://www.geogebratube.org/student/m19092

Sherman the Pig investigation (John Golden):

http://www.geogebratube.org/student/m170253

Minds on Mathematics - Storify

This is a record of the live-tweeting at @wendywardhoffer's #mindsonmath presentation at Kent ISD on Oct 2, 2014. In attendance and actively tweeting: @delta_dc, @ProfJonh, @RAnderson_Math.

Never Say Anything a Kid Can Say

Ever had one of these days?

If so, check out this article by Steve Reinhart (2000): “Never Say Anything a Kid Can Say!”.

For any fellow teacher-educators who view this, here's the home workshop I used to scaffold the discussion of this article, plus a few highlights from my students' post-workshop reflections.

Mr. Aion's Pledge to Improved Mathematics

I had to share this little gem I found on Year 2, Day 12, Justin Aion's blog, Relearning to Teach:

 

And so on his behalf and in his honor, I proudly present, "The Pledge to Improved Mathematics"! (also available in .png, .docx, and .pdf formats)

---

Image credit: Justin Aion, http://whiteboardmath.blogspot.com/

From the Syllabus: My SBG Blurb

 It is getting on toward the end of the 6-week summer semester in college algebra, and I am once again thinking hard about my standards-based grading (SBG) implementation. As part of my reflection, I looked back at the relevant sections of the syllabus, where I spelled out in some detail what I thought my students needed to know about my SBG implementation this semester, including a bit about the philosophy, the implications, the expectations, and classroom procedures.

In event that some of it may be useful to other educators embarking on the SBG journey, and in the hope that others will share their ideas and insights, here are those relevant sections of the syllabus:

Transformations

Or: Is this the kind of problem where you can have more than one answer?

There are a select few topics in algebra that can get me tied up in knots. One of those is function transformations--you know, horizontal & vertical shifts, vertical stretches & compressions, and horizontal & vertical reflections--specifically, those that involve a multiple transformations.

Here's the task I got hung up on the other day:

The graph of a function f is shown. Sketch the graph of y = 2f(x+1) - 3.

On these types of tasks, it's not the transformations themselves that get me. There are three transformations at work here, and I can describe them easily enough:

1. Horizontal shift one unit left (because of the x+1).
2. Vertical shift three units down (because of the -3).
3. Vertical stretch by a factor of 2 (basically, double the y-values). 

The part that gets me hung up, at least when I have not done these kinds of problems in a while, is... in which order should I apply the transformations?

Because it makes a big difference! To illustrate, let's trace where the point (-2,1) ends up if we shift-then-double vs. double-then-shift:

• Shift-then-double: (-2,1) --left1--> (-3,1) --down3--> (-3,-2) --double y--> (-3,-4).
• Double-then-shift: (-2,1) --double y--> (-2,2) --left1--> (-3,2) --down3--> (-3,-1).

See? (-3,4) and (-3,-1).. we end up in two different spots.

This is not "the kind of problem you can have two different answers to" (Cathy Humphreys; clipped from one of the videos in this book).

GVSUMath Youtube Channel - Brief Tutorial

You can follow these instructions to search for a specific math topic on the GVSU Math YouTube channel. (Last updated: 6/24/2014)

1. Go to https://www.youtube.com/user/GVSUmath/ and click the icon to expand the search box.

2. Type in a few key words...

3. ...and hit Enter. With any luck, we will have a video on the topic. Enjoy!

My tweets to #ed331 (Winter 2014)

This is a PDF printout of my tweets to the #ed331 hashtag for Winter 2014. You may also view the saved search Twitter's website.

When will I use this? (Laws of exponents?)

The Question: 

I received the following email from my Mom the other day. (She's been a middle school teacher since the early '90s). She wrote:

Jon, I received The Question today from one of my 7th graders today: "When am I ever going to need to know how to do this???" He is working on zero and negative exponents and had to solve problems like this:

Write an equivalent expression for 

The answer was

He understands how to do the problems--just wants to know why he needs to know, why it's not a waste of his time.

My Response:

Good questions! I wrote a blog post about the matter... let me know what you tell him. I'd love to hear how he responds.

http://profjonh.blogspot.com/2014/05/when-will-i-use-this-laws-of-exponents.html

That Blog Post (AKA, This Blog Post):

My colleague answers that question this way:

I don't know when or if you will ever need this particular concept. It depends on what you do with your life and what technological advances are made in the future. But you know what you will need to be able to do, regardless? You will need to problem solve. You will need to think critically (reason and prove). You will need to be able to communicate quantitative thinking to others. You will need to use representations to support your thinking and share your thinking. And you will need to make connections in order to consolidate your understanding. Mathematics is a discipline that provides opportunities to practice and strengthen all of these skills. So, as we solve for x, I want you to monitor your thinking because that's what's really important.

(Read his full blog post at: http://deltascape.blogspot.com/2012/05/when-will-we-ever-use-this.html)

He's talking about the Process Standards from NCTM (2000), which are now reflected in CCSS Standards for Mathematical Practice:

But just in case that argument doesn't satisfy your young math skeptic, you might want to share the following list of websites with him (see below). It turns out rational exponents are at the heart of a great many useful scientific formulas, not to mention a lot of really cool (and really beautiful) mathematics!

Good luck!
- Jon

Seven applications of rational exponents:

• Chemistry:
     http://chemwiki.ucdavis.edu/Physical_Chemistry/Kinetics/Rate_Laws/The_Rate_Law
• Modern Physics (Albert Einstein):
     http://en.wikipedia.org/wiki/Mass%E2%80%93energy_equivalence#Mass-velocity_relationship
• Classical Physics (Isaac Newton, born on Christmas Day, 1642!):
     http://www.logrog.net/users/lkovach/physics/Universal%20Gravitation/Days%201-3.pdf
• Rocket Science:
     http://exploration.grc.nasa.gov/education/rocket/isentrop.html
• Astronomy:
     http://scioly.org/wiki/images/c/c6/Formula_Sheet.pdf
• Wall Street investment trading:
     http://fr.accuracy.com/visuels/28t-1271338388.jpg
• Renewable Energy (Wind):
     http://www.raeng.org.uk/education/diploma/maths/pdf/exemplars_advanced/23_wind_turbine.pdf

Installing Cabinet Hardware (or, Fun with Fractions)

So I was installing cabinet hardware today...

...and some math happened! See, I had measured one drawer to be 17+3/8 inches wide. To place the pull correctly, I needed to find the center line of the drawer. So I needed to divide 17 3/8 by 2... not exactly compatible numbers.

Let's look at a few of my options.

Option 1: Use a calculator. 

My laptop is sitting right here. It has a built-in calculator:

Guest Post: The Value of Social Media for Teachers

The following is a reflection written by one of my preservice elementary mathematics teachers (@hollikathryn14) in W14, wherein she summarizes what she learned from an hour of professional development time spent with #MSMathChat on Twitter.

For some background on the assignment, see my post: Professional Growth for (New) (Math) Teachers.

When I read her reflection, I was inspired. I thought she nicely captured the power of looking to social media for professional development, and I hoped that her experience and perspective (pre-service teacher, and Twitter newbie), might inspire others to give it a try.

She graciously granted her permission for me to share this with you. And so, here's Holli's reflection on her first #MSMathChat experience:

Professional Growth for (New) (Math) Teachers

(Note: I wrote this post for my preservice teachers looking to complete their required professional development experience for my course(s), but then I thought: why not make it general enough to share with the world? I have also tagged it under the cognitive coaching label because it parallels the structure of a coaching conversation: reflect on your goals, set a focus for growth, articulate an action plan, implement it, and reflect on what you have learned.)

Looking for meaningful professional development? Have you tried Twitter? If not, I hope this post might help you (a) decide where you want to go and (b) learn about some social media options for getting what you need.

First, if you haven't already, I suggest you spend a few minutes brainstorming what you want to learn more about: 

• What are some of your strengths? 
• What are some areas where you want to learn more? 

It can be hard to hold yourself still... try setting a timer.

Look back over your list: What stands out to you? What are your priorities? What do you most want to learn more about? Set some goals for your professional growth.

Reflecting on Your Professional Learning

(Note: This post was created as a continuation of the post "Professional Growth for (New) (Math) Teachers", but it is general enough to apply to any recently professional learning experience.)

---

How do you reflect after a professional learning experience?

You might begin by responding to a few good questions, like: 

• How has your thinking changed? 
• What is important for you to remember from the experience? 
• How does what you learned align with your personal goals?
• Who else needs to learn this?

That last one is huge! If you have a blog, consider writing a post so that your learning becomes public and permanent.

If you don't have a blog, maybe it's time to start one? If so, help is available.

Here are two nice options for framing a written reflection:

Option 1: What, So What, Now What?

• What have you learned?
• So what? How will that impact your practice? 
• Now what? What do you want to learn next?

Option 2: Mirror the Reflecting Conversation structure from Cognitive Coaching.

• How did it go?
• How do you know?
• Why is that so?
• How did you grow?
• How did this help you know?

Hey, congratulations on your new learning!
Now... what's next for you?
 

Is there a problem here?

Is there a problem here?

from Doug Fisher's Michigan Reading Association Presentation (via delta_dc)

A student in my W14 teacher-assisting seminar raised this question:

If the [desirable] Japanese lesson style* is all about posing meaningful problems and allowing students to explore them, and if the proper role of the teacher is to lend perspective and support in those investigations, then why are we taught to use gradual release of responsibility?
  * we might substitute problem-based learning, or 3 act lessons, or active inquiry, or...

Then today (4/9/14) I read this on Twitter from @ZPMath.

Portfolio Feedback (ED331 W14)

See below for feedback codes on the ed331 portfolio.
Also, here's a link to a sample portfolio that might be useful: http://ed331portfolio.weebly.com/

April Fool's Math: Pythagoras Who?

Some of my #ed331 teacher assistants have posted lessons they have taught -- to actual students! -- in which they supposedly prove the Pythagorean Theorem. You know:

For any right triangle, the sum of the squares on the legs is equal to the square on the hypotenuse. Sometimes folks just shorten it to a^2 + b^2 = c^2.

I know, right? Prove the Pythagorean Theorem!? No way.

Here's one example from @kayfayayyy's blog--she thinks she's going to be a math teacher one day--except here she is, showing her students a supposed 3-4-5 right triangle. Oh yes, very clever Miss Fayayyy (if that's even your real name).

You've learned your lessons well: just dangle some candies in front of your kids and they'll believe anything you say. You can read more about her lies at her blog if you like.

But what Miss Fayayyy doesn't know about candy is that it likes to play both sides. How about this 3-5-6 right triangle?

Go ahead, count the Skittles. 9 + 25 = 36? No way, man. There it is: a counter-example, in all its Wild Berry flavor glory. We must conclude that the Pythagorean Theorem is false.

Recognizing Our Implicit Assumptions

I'm reading The Teaching Gap with my EDI 331 students (again) this semester. Every time I read it, I find something different that stands out for me. First, it was the perspective I gained by comparing "typical" lessons from Japan, Germany, and the U.S. The second time, it was focus on improving teaching rather than improving teachers, which coincided with all the voices in 2012-13 clamoring for attracting better, smarter, more biz-savvy people into the teaching profession, because--the voices loudly proclaimed--the teachers we have now are just not cutting it.

This time around, what struck me was the discussion of the culturally embedded assumptions of what it means to "teach, learn, and do mathematics".

Some of my students have been tweeting about that:

Reading #TTG ch6 has me thinking bout how teachers can effectively promote worthwhile change in stnd script #ed331 pic.twitter.com/YiSQA6LxuP — Dominic Taylor (@DominicTaylor11) March 7, 2014

With that context, let's get on with the post.

SBG Targets: Rubric or Checklist?

As I prepare learning targets for my next unit of instruction, I am contemplating whether it might be useful to split my targets into two categories: Checklist Targets and Rubric Targets.  

Reflecting on your Coaching Session

When I supervise student teachers and teacher assistants, I use cognitive coaching to frame my classroom visits. Students fill out a pre-observation action plan, using their goals for professional growth to identify a focus for the observation.

After the observation, we use a coaching reflecting conversation to reflect on the lesson and construct new learning. Students then reflect on the process by writing a blog post on the subject.

They are invited to use one of two formats for their written reflection:

Option 1: What, So What, Now What?

• What? What are some of your main takeaways?
• So what? Why are those important to you? 
• Now what? What are the implications? How? When? Who?

Option 2: Mirror the reflecting conversation framework.

• How did it go? (Were you successful? How do you know?)
• Why was it so? (What caused it to go that way?)
• How did you grow? (What have you learned? How will you apply this in the future?)
• How did this help you know? (Be meta-cognitive: Reflect on the process.)

Here are a few sample posts from a few of my students to show how this might look.

• From @rwhite21793, a post titled: Reflections on My Teaching!
• From @KelseyJohnsonGV, a post titled: First in-school Coaching Observation 
• From @DominicTaylor11, a post titled: Fun Classroom Management?
• From @KalieGVMath, a post titled: What? So What? Now What? (Round 2)

So, how do you go about reflecting on your teaching?  

Coaching Session - Who's Engaged?

I recently completed a couple of classroom observations with student teachers who had identified student engagement as one of their personal learning goals on the action plan for the observed lesson. We agreed I would collect data on student engagement at five-minute intervals using an annotated seating chart.

Here's the diagram from one of the classes. Letters "A" through "H" mark students who I judged were not on task at at least some point during the five minute time index of the survey.

What do you notice? What questions do you have?

Here's the diagram from another class at a different school. The seating arrangement shifted mid-lesson when students began to work in pairs; these pairings are indicated as bolded connections on the diagram. 

Again, letters "A" through "H" mark students who were not on task at that time index of the survey. You can see a chronicle of this lesson below the chart.

How Am I Doing? EDI 331, W14

In EDI 331 - Mathematics Teacher Assisting, I engaged each of my students in a one-on-one Cognitive Coaching session aimed at setting goals for their teaching practice this semester. I have found that setting goals focuses my efforts, and I make an effort to set two or three explicit goals for every course I teach.

Well, I have been having my students blog about their teaching goals, so I thought I might take some of my own medicine and share mine too. So, without further adieu...

My goals for EDI 331, W14 are:

1. To provide home workshops that are relevant, useful, and engaging.
2. To make sure our in-class workshops connect with the home workshops and extend them in a meaningful way.
3. To foster appreciation for the math-twitter-blog-o-sphere as a means of professional growth.

If it's not graded, I won't do it

One task all faculty at GVSU are asked to do every February is prepare an annual Faculty Activity Report (FAR). This entails compiling a complete list of our efforts for the past calendar year in the areas of teaching, scholarship, and service.

Our procedures are a bit more involved than this...

One piece of our FAR includes a reflection on trends we have noticed in our student evaluations of instruction. A colleague who had read my teaching reflection invited me to share the following in the hope that others seeking to make sense of and respond to student evaluations of instruction might find it useful.

Crowd-sourcing Our Midterm Review

I had to take a sick day today, so we are reviewing for our Mth323 midterm exam by crowd-sourcing a review guide. Students have been asked to add at least two tips for our learning targets, plus as many questions as they have. Check it out (updated every 5 minutes or so):

SBG at Math in Action (2014)

Here are the slides from my talk at the 2014 GVSU Math in Action Conference.

---

SBG has grown too big for this post! To access my growing collection of learning targets, presentations, and links to a variety of SBG resources, please visit the new Standards Based Grading page.

---

A Question of Balance

This post is based on a student comment that caught my eye while grading. The data below shows the sodium content (in mg) for 23 brands of "regular" Peanut Butter.

The student wrote one of the following two statements in defense of choosing the preferred measure of center.

1) The data are balanced on each side of the median.
2) The data are balanced on each side of the mean.

Which statement do you think is more correct? In what sense might someone think the other one is correct, too?

Ready... GO!!

Why Precision Matters

The following home workshop was used with preservice teachers in an effort to highlight the importance of attending to precision when doing mathematics investigations.

Home Workshop - Angles of Polygons by hasenbaj

How might you improve?

How convincing is this? How might you do better?

These questions were bothering me. I had just completed a paper with colleagues Lenore Kinne and Dave Coffey on the effective use of rubrics for formative assessment (in press). In it, we wrote:

...a good rubric provides feedback on the progress that has been made toward the goal while simultaneously communicating ways the performance might be improved (emphasis added).

My rubric did the first part, but it bothered me that it didn't do the second part.

For that, I had to write comments on students' papers. I realized I was writing the same sort of comments over and over. I needed to do something about that.

Those Less Convincing Performances

I recently completed my second semester of standards-based grading. I have learned a lot, and will try to post more about that this semester.

After a conversation with a colleague, Pam Wells, about the SBG system I'd been using. The conversation got me thinking about how to handle the, shall we say, less convincing performances. 

Email to Pam on the matter:

Pam, I appreciated the opportunity to talk with you about SBG on Friday. Since then, my thought keep returning to the rubric and the question of what a “1” means. I think I will change how I use 1’s in the future.

When we talked, we agreed that 1 basically means “you don’t get this yet.” In that sense, a 1 should not count as evidence of proficiency at all. So a 1 and an 0 are similar: they mean “no evidence provided”, but for different reasons. Anything at a 0 or 1 simply does not count as a piece of evidence for that target. If we require two pieces of evidence for each target, this reinforces the mastery mode of grading implicit in SBG. If you don’t get to two pieces of evidence, the grade is reduced.

Volume & Surface Area.. or, Wrapping Pancakes

We had pancakes tonight. And we had leftovers. So we decided to store them in the fridge to reheat later.

This is the way you are supposed to do it. 

But we just wrap them in foil and stuff them in the fridge. So, as usual, I pulled out a sheet of aluminum foil, eyeballing how much I would need and adding another inch or two for good measure.

Then I stacked the pancakes on top. It looked like this. (Ok so far...)

Two side-by-side stacks, and one extra on top. (That's odd...)

But then I folded up the foil, and that looked like this.

My tweets to #m432 (Fall 2013)

This is a PDF printout of my tweets to the #m432 hashtag for Fall 2013. You may also view the saved search Twitter's website.