Recognizing Our Implicit Assumptions

I'm reading The Teaching Gap with my EDI 331 students (again) this semester. Every time I read it, I find something different that stands out for me. First, it was the perspective I gained by comparing "typical" lessons from Japan, Germany, and the U.S. The second time, it was focus on improving teaching rather than improving teachers, which coincided with all the voices in 2012-13 clamoring for attracting better, smarter, more biz-savvy people into the teaching profession, because--the voices loudly proclaimed--the teachers we have now are just not cutting it.

This time around, what struck me was the discussion of the culturally embedded assumptions of what it means to "teach, learn, and do mathematics".

Some of my students have been tweeting about that:

Reading #TTG ch6 has me thinking bout how teachers can effectively promote worthwhile change in stnd script #ed331 pic.twitter.com/YiSQA6LxuP — Dominic Taylor (@DominicTaylor11) March 7, 2014

With that context, let's get on with the post.

I get these emails from companies every so often (read: almost daily) that claim to have found the solution to students' challenges with learning mathematics.

The one I got today from Hotmath.com:

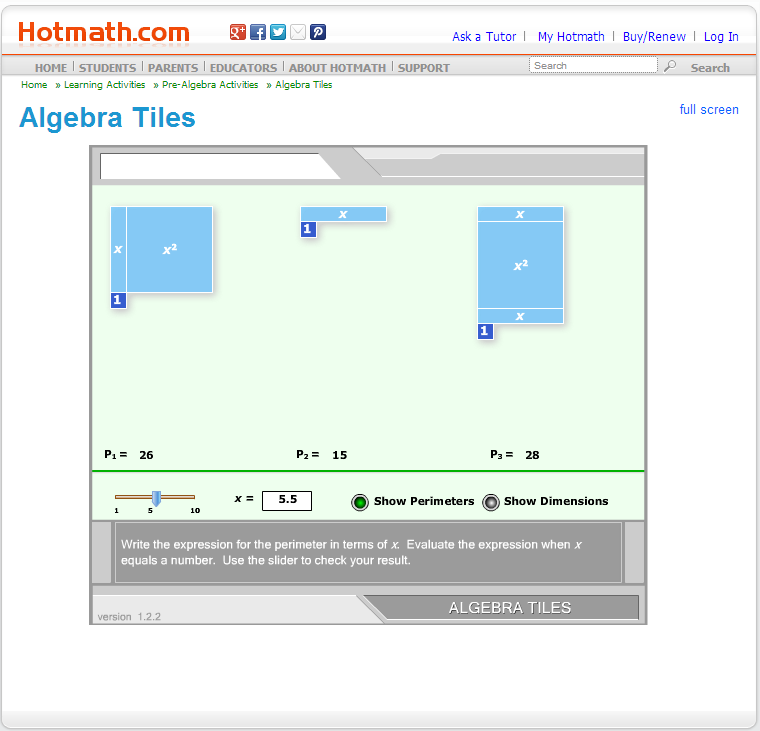
The top link in the email takes you to this Flash applet:

I took a moment to play around.  You might want to do that too. Watch for hidden assumptions. Be sure to come back when you are finished!

Whew, you came back. Thanks. Did you notice any hidden assumptions about teaching, learning, and doing math?  

Let me see if I can help share some of the ones I noticed, and illustrate what The Teaching Gap concludes reflect deeply ingrained cultural beliefs, with this brief vignette:
---

Student 1: Let's look just at the one in the top left. The directions tell us to "Write the expression for the perimeter...".

Student 2: But wait, the expression? There's only one? 

S1: I assume they probably mean the one you get when you apply the formula P = 2L + 2W. Here, L = x+1 and W = x. So we get:

P = 2(x+1) + 2(x)

S2: Ok, so that's the expression for perimeter. That was easy.
S1: Wait, we're done, right?
S2: I guess so. I mean, it seemed pretty easy. 
S1: Yeah. Too easy. Maybe we better simplify it. 

 ---

So far, here are some of the assumptions I see. These ideas are adapted from The Teaching Gap's characterization of U.S. cultural assumptions about the nature of mathematics.

• U.S. Belief 1: Math is a set of procedures. 
• U.S. Belief 2: Being good at math means consistently getting the right answer.
• U.S. Belief 3: Practicing procedures is boring. The teacher should make it fun!
• U.S. Belief 4: Math is hard. The teacher should make it easy! 
• U.S. Belief 5: Different students think differently; those differences present challenges that teachers must overcome if they are to help all students learn.

The assumptions are implicit in the way the applet is structured. For instance, it asks:

• What's the correct expression? (belief 1, belief 2)
• Use the slider to check your answer (belief 2)
• Using the applet makes doing math interactive, easy, and fun (beliefs 3 and 4)
• If you need help, just click the buttons (belief 4)
• Using the applet makes it easy to differentiate instruction (belief 5). 

What if we move beyond those assumptions? What might that look like?
---

P = 2 + 4x

S1: I wonder if we see this another way... Yes! Check this out. I can see it as two 1-unit lengths and four x-unit lengths.

S1: Do you see it yet? Look at my diagram...
S2: Oh, yes, I see that now.

S1: I wrote this expression for perimeter:

P = 2 + 4x 

S2: Yes, that makes sense. Is it correct?I think so. Is it equivalent to yours? 
Maybe, let's check.

S3: Wait! I saw it another way!

Seeing P = 4x + (2x+2) - 2x

S2: You got a different answer?
S3: Yes. Look at my picture. Can you see what I'm thinking? 

S3: I get this expression for P:

 P = 4x + (2x+2) - 2x. 

S1: I think I see it. Is that right, too? 
S2: I wonder if all three of our expressions correct?
S3: Right. They all make sense when we explain them.
S2: I bet they are all equivalent.
S1: Let's find out.

---

The applet's hidden assumptions are particularly visible when held up against the backdrop of the Japanese cultural beliefs about mathematics, summarized below from the analysis presented in The Teaching Gap.

• Japan Belief 1: Math is a set of relationships. 
• Japan Belief 2: Being good at math means being good at thinking in new and creative ways.
• Japan Belief 3: Math is an intellectual challenge, worthy of productive struggle.
• Japan Belief 4: Confusion and frustration are natural and beneficial.
• Japan Belief 5: Different students think differently; those differences produce unique objects of thought that we can mine for hidden relationships.

So, what implicit beliefs and assumptions might have influenced your experiences with teaching, learning, or doing mathematics?